本篇想要介紹的是《反脆弱》這本書的核心概念。
切入的角度是從本書的副標題——Things that gain from disorder,當初看到這句話就覺得很神奇,為什麼有事物會從混亂中受益?
穩健、脆弱與反脆弱
這就要先從作者的職業生涯談起,作為一位交易員,他觀察到將投資組合的報酬呈現在時間軸上,主導整體報酬的,往往不是大多數的事件,而是罕見但份量非常重的事件。
時間軸
這裡作者觀察三種系統在時間軸上的表現。
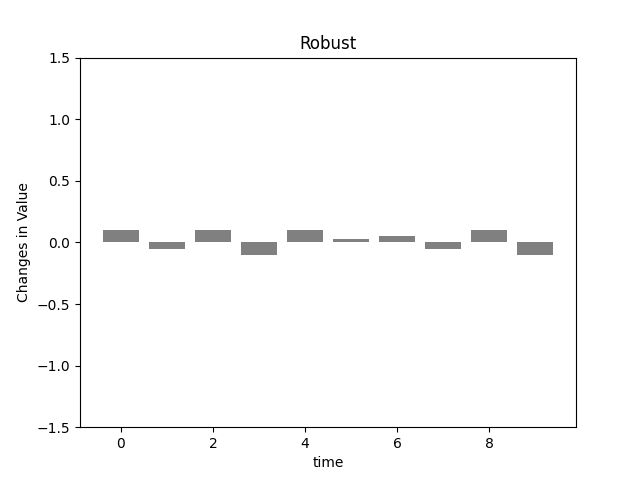
- 左邊的表現是穩健(robust),這個系統不論外界事件如何波動,都不會大幅被影響,如果是一個投資組合就是不會大賺也不會大賠。
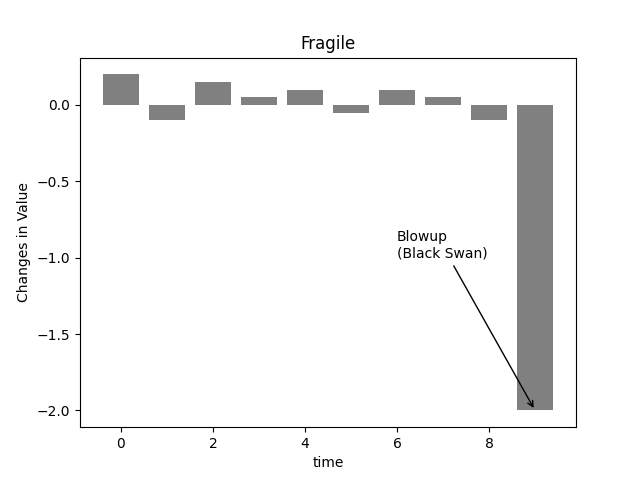
- 右邊的表現是脆弱(fragile),這個系統在罕見的突發事件發生時(黑天鵝事件),可能會直接崩盤。
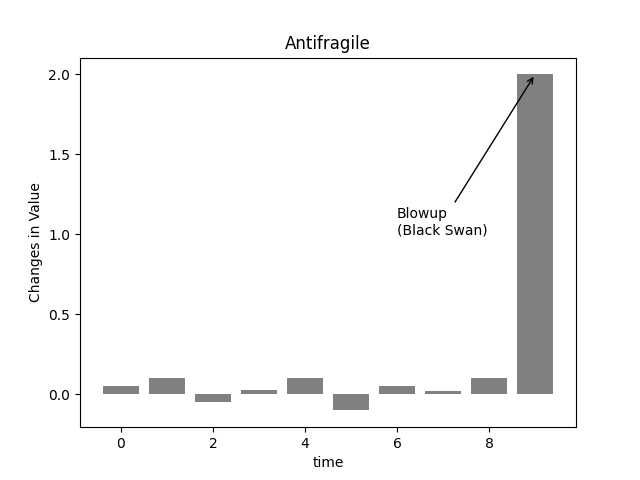
- 上圖就是本書作者感興趣的反脆弱(antifragile)系統,在罕見的突發事件發生時,不但沒有崩盤,甚至還獲得大幅利益。
作者在這裡用了反脆弱這個詞,是因為他認為一般人對於系統面對混亂時的表現,只有「脆弱」與「穩固」兩種想法,但是身為一個交易員,卻常常觀察到因為波動而受益的例子,他認為脆弱的反面不是穩固,而是反脆弱,因此才建立這個概念和名詞。
機率分佈
剛才我把報酬沿著時間軸呈現,而如果把報酬放在x軸,而y軸表示發生的頻率畫成分佈,可以更清楚看到三個系統的差異。
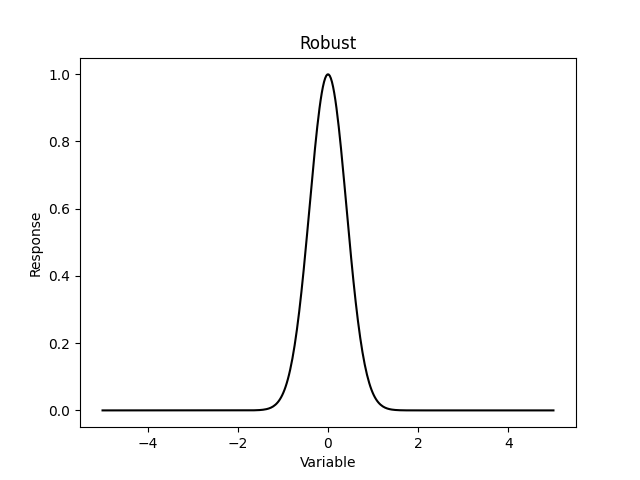
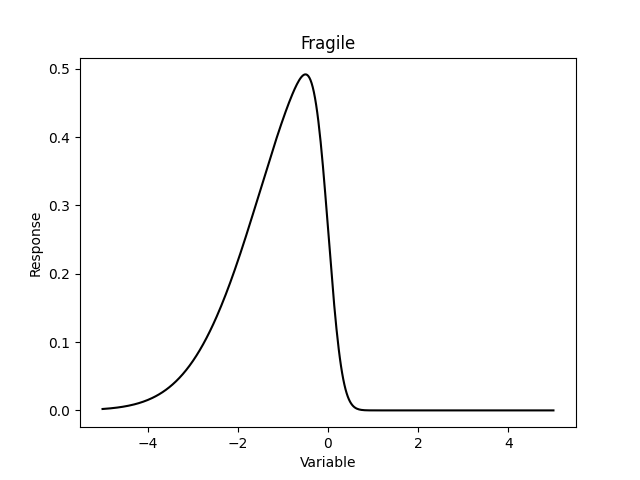
- 左邊的穩健系統,其分散程度較小,因此不確定性低,大部分事件都是在平均數附近發生,而利得與傷害發生的頻率是相等,所以整個分佈是對稱的。這很符合我們對一個穩健系統的想像,也就是不論外界事件如何波動,都不會大幅被影響。
- 右邊的脆弱系統,可以看見分佈在左側有厚尾但右側沒有,這表示負報酬(傷害)比正報酬發生頻率要高。
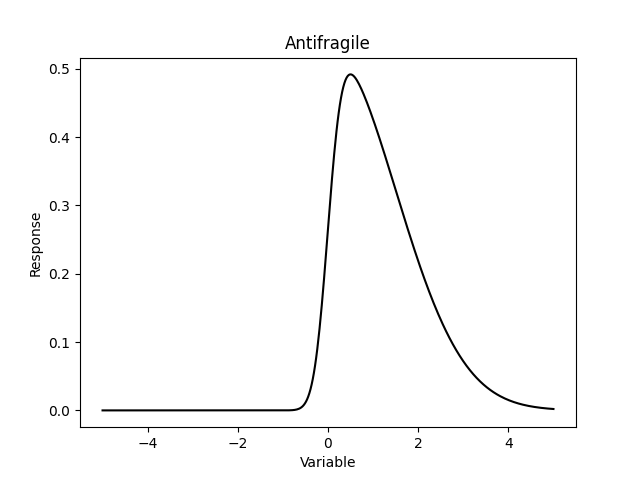
- 上面的反脆弱系統,可以看見分佈在右側有厚尾但左側沒有,這表示正報酬(利得)比負報酬發生頻率要高。
看完這三種系統在時間和頻率分佈上的表現後,我們便忍不住發問:世界上哪有這種好事?又是什麼樣的機制導致系統會呈現這樣的特性?
槓鈴策略 (Barbell Strategy)
秘密就在反脆弱系統具有一種稱作槓鈴的結構,其實直觀的概念很簡單,就是隱惡揚善——去除不喜歡的,留住喜歡的部分。
所謂槓鈴結構在投資組合中很常出現,面對時時變動的市場,一個投資組合中通常會由「極高風險極高報酬」和「極低風險極低報酬」,這兩種資產組合而成,而避免集中以風險中等的資產為主。
這是因為如果所有資產都集中在中段,結果罕見事件發生時才證明了這些資產並非中等風險,這時候整個投資組合便崩盤了。
但是如果投資組合是由極高和極低兩種資產構成,則極高風險的資產就算全滅,最慘的狀況已經由比例控制住了;但是當市場大漲,又能夠參與高風險的資產帶來高報酬。不過前提是極低風險的資產必須真的是極低風險,但這會比評估什麼叫做「中等」風險還更容易一些。
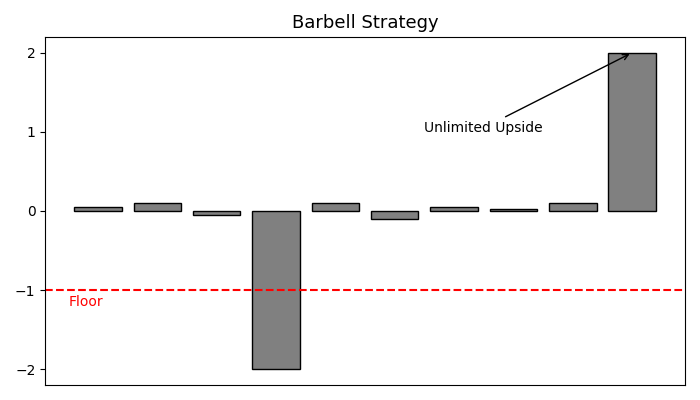
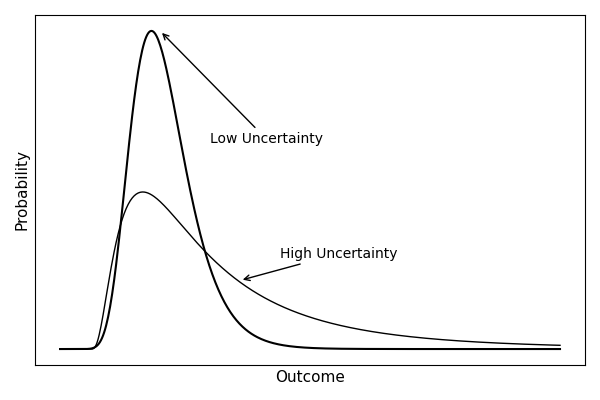
回來看這樣的系統在時間軸與分佈上的表現,可以看到這就是讓下檔風險(downside risk)有一個下限(左圖的floor紅線),這讓一個系統在最糟情況下的損失是有限的;而上檔利益(upside gain)則沒有限制。
有了槓鈴策略之後,在右圖分佈也可以看到,當不確定性低的時候分佈都聚集在中間,但是當不確定性高的時候,右側的厚尾就出現了,代表這個系統享有上檔利益;而左側沒有厚尾,是因為損失被下限擋住了。
非線性
上述這種「限制下檔風險,保留上檔利益」的槓鈴結構,造就了報酬的不對稱性,然而目前好像只覺得在投資組合的例子上合理,但對日常生活的隨機性,比較不容易看出「限制下檔風險,保留上檔利益」怎麼可能做到?
作者接下來就要帶出核心的理論,把一切都串起來,也就是這世界上處處存在著對事件的非線性反應。
首先我們把前面用到的詞語寫成定義:
- x: 事件(event)是隨機性的來源、混亂、不確定性
- f(x): 對事件的暴露程度(exposure to event)、反應(response)、報酬(payoff)、結果(outcome)
區分x和f(x)是重要的,因為x是隨機事件的分佈,可以想像就是每天會發生在我們身上的幸運事和各種鳥事。但我們通常真正關心的是f(x),也就是對我們的影響,前面沿著時間軸和機率分佈呈現的都是f(x)的狀態,而不是x的狀態。
所以關鍵就在於,x是怎麼變成f(x)的?答案就是非線性的轉換,特別是凸性轉換 (Convex Transformation)。
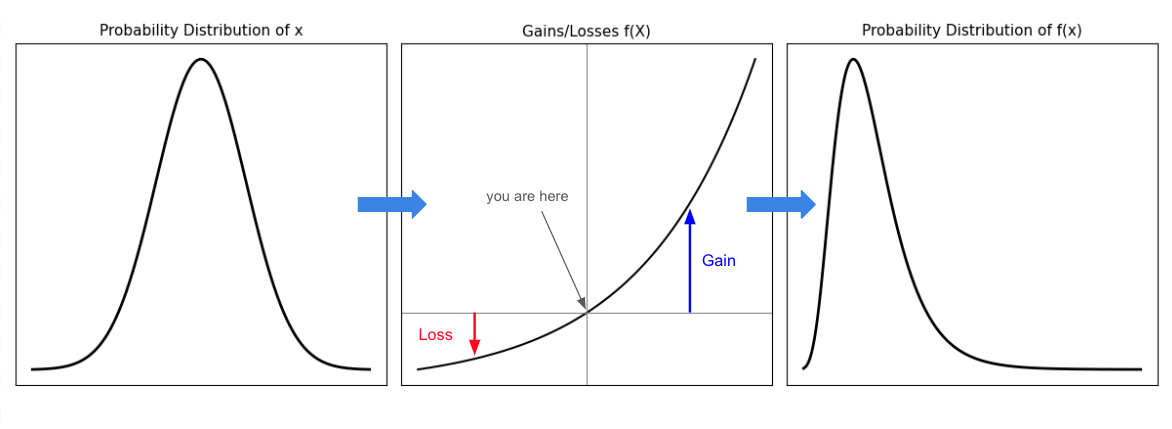
以上圖為例,是凸性轉換將一個隨機事件的分佈,轉換成一個不對稱的分佈,也就是我們前述看過的反脆弱分佈(右尾肥大但左尾被截斷)。作者稱凸性轉換為現代的點金石,比擬為古代煉金術化朽土為黃金的關鍵要素。
這個世界到處都存在非線性的關係,像是x是車流量而f(x)是通勤時間、x是股票市場的波動而f(x)是報酬、x是專案的複雜度而f(x)是專案所需要的時間…。這些關係都不是線性的,也就是事件x的大小不會等比例的出現在結果f(x)上,而是隨著規模越大而呈現非線性的成長。
作者提到將x與f(x)混淆,是常犯的錯誤,低估實際的反應是非線性成長:
- 以為關閉一條道路,通勤時間只會線性的增加,結果關閉一條道路造成大塞車
- 預估專案完成時間時,用各個部分預估時間的總和估計,結果組合起來複雜度大增,所需要的時間非線性的增加
擁抱隨機性
凸性轉換把前述的槓鈴擴展了,因為槓鈴結構在做的就是凸性轉換,透過設計暴露風險的部位,得到類似凸性轉換的結果。
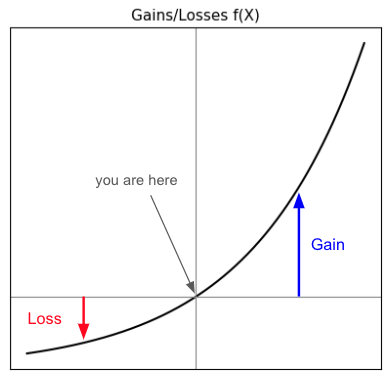
從上圖凸性轉換的例子,就可以緊扣回Things that gain from disorder這個副標題,如果你對於隨機性的暴露呈現凸性,你當然會喜歡隨機性,因為隨機性將你帶離中段。以上圖為例,上圖x是0的位置f(x)也是0,但是x具備隨機性而開始波動,就會產生損失與利得,然而把損失與利得累計的結果平均,會大於0,這就是Jensen’s inequality。
隨機性會帶來傷害沒錯,但只要利得(藍線)大於損失(紅線),長期下來你可以承受多次的小損失,但只要一次利得就足以補償所有的損失,甚至還遠遠超過當初損失的量。
既然凸性轉換就是把隨機性當作母牛(作者用milk uncertainty這個詞很生動),所以問題就是:到底要怎麼讓自己處於這個凸性結構?
試誤法是一種隱藏的選擇權
這邊所有理論就告一段落了,剩下就是行動的部分。
上述這個脈絡告訴我們,凸性遠遠比預測正確或是擁有知識還要重要,當一個系統處於凸性,不需要用知識、資訊去預測隨機事件,因為這個有利的結構,長期而言能夠抵消所有的累積傷害。
作者甚至認為預測不是中性的,不但無效還帶來錯誤的行動,會影響決策、鼓勵干預而造成傷害,這種假性的知識比起單純錯誤還要嚴重。
這也正是選擇權的精髓所在。購買選擇權,就是以少量的權利金換取未來的潛在權利;當市場朝預期方向上漲時,選擇權的價值便隨之提升。而倘若市場走勢不利,最多僅損失當初支付的少量權利金,因此,這是一種「限制下檔風險、保留上檔利益」的投資機制。選擇權不是仰賴能夠預測市場作為前提才獲利,而是因為它本身的結構就是一種凸性轉換。
但是人生又不是金融市場,哪有這種顯性選擇權操作?作者就提到了人生有許多的隱藏選擇權,而試誤法(Trial-and-Error)試錯的成本很低,可以讓人迅速得到回饋做出下一步修正,而如果成功,則可能獲得巨大的報酬,因此試誤法就是一種選擇權的結構。
這好像很直觀,但這完全不同於學校的立場,過去的教育建立在一種「需要理解理論,再去推進實務」的觀念,這種信念引導學習知識、吸收更多資訊、全盤理解、對未來進行預測,最終才是行動,然而作者認為真正的知識和創新是試誤法拼湊的結果,倚賴的是凸性轉換,而非理想的知識建構。真正推動世界的,是在實務過程中累積的隱性知識,因為行動逼迫人專注在生存關鍵上思考,而不是過度複雜化而忽略重點。
反脆弱的不確定性指南
別試圖預測和解釋事件,應該把重點放在辨識系統對於事件程度加劇的變化(i.e. f(x)的非線性反應),因為變化通常比實際上的數值容易估計,像是體重計壞掉(無法知道實際的數值)但你還是可以知道自己正在變胖(可以偵測變化率)。用這種思維能夠建構一個能夠在隨機性中成長的系統。
最後作者也做了個小總結:
- 把每個機遇看成是一種選擇權
- 投資於人、而非計劃,因為人可以調整,然而計劃容易陷入一種敘事
- 不管在什麼領域,都記得保有槓鈴,避免毀滅
後記
這本書的內容非常豐富,我只把比較有印象的一小部分寫出來。作者在論述帶了很多例子和典故,而且文筆很幽默、犀利又批判性強,很愛其中對理性的批判和對於倫理的承諾,絕對推薦有空來實際讀讀這本書!